Family tree project - convert sub-graph to list
Sep 1, 2019When I started to create the family tree project I chose the dTree visualizing library. To visualize a family tree with the dTree you have to provide the data in a hierarchical format:
Parent1:
Marriage:
Parent2
Childs...
Child1
Child2
Marriage:
PersonX
Childs:
...
...With this data format, it’s not possible to save multiple family trees. Also, it’s only possible to render one parent history with the dTree library (I think the cause is graph overlapping).
But I wanted to have the possibility to save multiple family trees (for Parent1 and Parent2) in one data structure. The rendering of multiple family trees at one time wasn’t important to me.
So I created a (graph) data structure that can be converted to the necessary dTree format.
Example graph data structure:
{
"persons": [
{
"id": 0,
"name": "Parent1",
"gender": "man"
},
{
"id": 1,
"name": "Parent2",
"gender": "woman"
},
{
"id": 2,
"name": "Child1",
"gender": "woman"
},
{
"id": 3,
"name": "Child2",
"gender": "man"
}
],
"connections": [
{
"partner1Id": 0,
"partner2Id": 1,
"childrenIds": [2, 3]
}
]
}With this approach it was possible to have multiple family trees in one data structure and extract the wanted family tree.
How to generate the sub graph
The flow of the algorithm is:
select a node
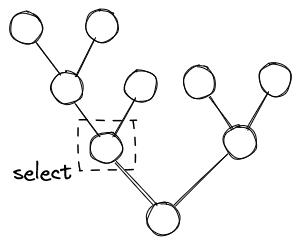
and follow the Parent A until there is no Parent A.
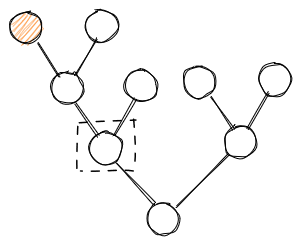
This is the root node from which a new subgraph is created (partner and children).
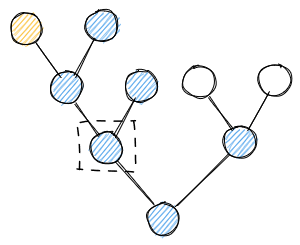
This subgraph gets transformed to a compatible dTree hierarchy.
Done 🚀